Анализ развития дополнительного образования в Новосибирске и области

Условиями осуществления интеграции могут служить:

- анализ потенциала учреждений дополнительного образования детей (далее - УДОД) в предоставлении дополнительных образовательных услуг;

- анализ возможностей ОУ в реализации внеурочной деятельности;

- построение содержательной линии образовательных программ основного и дополнительного образования.

Осуществление интеграции общего и дополнительного образования детей на уровне территориального образования возможно на основе принципов согласованности, комплексности, долгосрочности, разноуровневости. При этом направленность интеграции по образовательным областям (группам предметов) Базисного учебного (образовательного) плана для ОУ РФ должна быть выполнена.

Таким образом, мы видим, что происходит наложение, взаимопроникновение и взаимодополнение образовательных программ УДОД на типовые программы ОУ, и соответственно, от этого зависит какие цели, содержание, методы, формы и средства обучения необходимо учесть, для того, чтобы получить качественно новые результаты интегрирования.

Интегративный подход при разработке образовательных программ и проектировании организации образовательного процесса может быть выражен в следующей схеме (рис. 1):

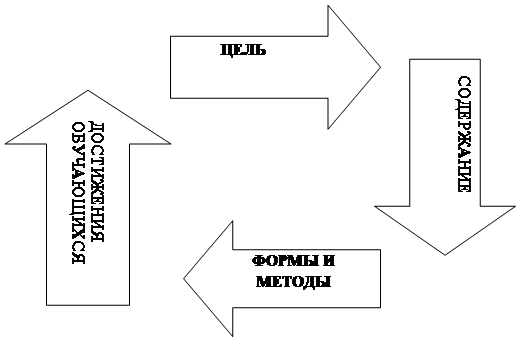Рисунок 1 - Согласование общих целей и механизмов реализации образовательных программ между ОУ и УДОД

В Новосибирске, а в большей части в Новосибирской области при детальном рассмотрении этого вопроса объективно существует ряд проблем:

1. Отсутствует практика обобщения и распространения передового педагогического опыта работы учреждений, педагогов по теме интеграции общего и дополнительного образования.

2. Не получили должного развития данное направление в работе методических служб муниципальных образований.

3. Существует проблема вовлечения обучающихся в проектную и общественно-значимую деятельность.

4. Сложно решаются вопросы мотивационных механизмов стимулирования труда педагогов, работающих в условиях интеграционного процесса.

5. Требует совершенствования система организации и управления этим процессом.

Однако верно сделанный выбор моделей интеграции позволяет обеспечить реальные результаты.

Результаты интеграции для обучающихся:

- увеличивает пространство развития творческой и познавательной активности;

- позволяет реализовать индивидуальную образовательную траекторию обучения;

- расширяет тематику изучаемого материала;

- демонстрирует способности, невостребованные основным образованием;

- увеличивает спектр учебных предметов;

- повышает роль самостоятельной работы;

- реализует лучшие личностные качества.

Результаты интеграции для образовательного учреждения:

- адекватность современным требованиям образования и воспитания;

Статьи по теме:

Требования, предъявляемые к качеству учебной литературы
Качество образовательного процесса во многом определяется содержанием и уровнем его методического обеспечения. Опыт методической работы в учебных заведениях позволяет констатировать, что проблемы с содержанием учебной литературы все еще актуальны. Содержание учебной литературы должно быть направлен ...

Проблема оптимальных сроков начала развития творческих способностей.
Говоря о формировании способностей, необходимо остановиться на во­просе о том, когда, с какого возраста следует развивать творческие способности детей. Психологи называют различные сроки от полутора до пяти лет. Также сущест­вует гипотеза, что развивать творческие способности необходимо с са­мого р ...

План-конспект урока по алгебре и началам анализа в 11 классе
Теме: «Показательная функция» Класс – 11 Цель урока. Повторить свойства показательных функций, способы решения показательных уравнений и неравенств Образовательные задачи: - применение алгоритма решения показательных уравнений и неравенств; - актуализация опорных знаний решения квадратных уравнений ...