Работа над текстовой задачей с использованием тетрадей с печатной основой

Затем можно предложить детям такую запись:

,

анализ которой позволит им сделать вывод о том, какого цвета были 3 шарика, и что такая запись показывает, что синие шарики положим обратно в мешочек, объединим все шарики вместе.

Исключительно важную роль в подготовительный период играют задания, представленные в тетрадях с печатной основой Н.Б. Истоминой. Выполняя задания, ребёнок приобретает навык внимательного прочтения текста, точного выполнения условий задания. Например, задание №2: У Миши 3 зелёных и 2 красных шара, а у Маши 6 зелёных и 3 красных шара.

Задания: а) Закрась столько кругов, сколько всего шаров у Миши:

б) Закрась столько кругов, сколько всего шаров у Маши:

Могут быть заданы дополнительные вопросы после выполнения заданий. Например, можно спросить:

а) Сколько красных шаров у детей?б) Обведи замкнутой кривой линией, на сколько у Маши шаров больше, чем у Миши?Например, в задании №4 даётся текст: «В коробке 8 карандашей. Из них 5 красных, остальные — чёрные» и предлагается выполнить следующее:

а) обведи кривой замкнутой линией столько карандашей, сколько их было в коробке: (дан стилизованный рисунок).б) Закрась красные карандаши красным цветом, чёрные — чёрным цветом.

Дополнительно можно спросить, например, каких карандашей в коробке больше (меньше) и на сколько; можно предложить схему:

и спросить, какие цифры надо записать в эту схему, чтобы показать, что чёрных карандашей 3 (или, что красных карандашей было 5).

А вот задание №6:

«В коробке лежат большие и маленькие пуговицы. Больших пуговиц столько: 9 – 6.а) Обозначь каждую пуговицу кругом и нарисуй столько кругов, столько всего пуговиц в коробке:

б) Закрась большие пуговицы красным цветом, а маленькие — зелёным.»

Опираясь на понятия части и целого, дети выполняют задания, определив, что всего пуговиц 9 (это целое), больших 3, маленьких 6 (3 и 6) — это его части).

Дополнительно можно предложить записать с помощью знаков, сколько маленьких пуговиц (9 – 3 — надо от всех пуговиц отнять большие пуговицы и останутся маленькие пуговицы); а что будет обозначать такая запись: 3 + 6?

Задание №7 ориентирует на запись данных, используя данное выражение и на схематическое изображение данных выражения с помощью отрезков.

На установление соответствия между графическими и символическими моделями направлено задание №7:

«Обведи на каждой схеме красным цветом отрезок, который соответствует данному выражению:

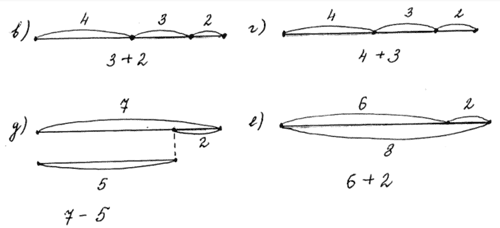
Дополнительно можно предложить составить к любой из схем текст (маленький рассказ с этими числами).

Задание №9 ориентировано на осознание состава числа 9 через выполнение рисунков и на возможность выполнения его разными способами. Можно спросить детей, какое ещё задание можно предложить к данному заданию (какие выражения можно записать к каждому рисунку?).

Все задания личностного ориентированы: «закрась:», «нарисуй:», «обведи:», «обозначь:», «запиши:», «посчитай:», «покажи:», «отметь:», «закончи рисунок:», «подчеркни:», «выбери:», «отложи с помощью циркуля:» и т.д. Учителю необходимо обеспечить условия для максимально самостоятельного выполнения этих заданий с последующим фронтальным обсуждением вариантов (правильных и неправильных) выполнения этих заданий.

Вся работа по учебнику «Математика 1» Н.Б. Истоминой в той или иной степени готовит детей к овладению умением решать текстовых задачи арифметическим методом. Но особенно ярко и целенаправленно формируется умение, о котором идёт речь, начиная с момента ознакомления детей с понятием «длина». Здесь учащиеся встречаются с текстами без числовых данных, например: «Вова выше Пети, а Петя выше Коли. Покажи на рисунке Вову, Колю, Петю». Или такое задание: «Красная лента длиннее синей, но короче жёлтой. Покажи, какая лента красная.» Здесь используются предметные модели или рисунки, вербальные, символические, а после ознакомления с отрезком — и графические модели. Здесь соотносятся рисунки с отрезками, например: «Догадайся, каким отрезком обозначено каждое дерево?» , «Как связаны рисунки с отрезками?», «Выбери два отрезка, которыми можно обозначить красную и синюю ленты».

Статьи по теме:

Задачи, методы и организация исследования
Задачи исследования. Сформулированная во введении цель работы позволила определить задачи исследования. Определить начальный уровень физической подготовленности у юношей IX и X классов. Обосновать эффективность использования силовых и скоростно-силовых упражнений на уроках физической культуры юноше ...

Психолого-педагогическая компетентность
Для успешного формирования социальной компетентности у детей с отклонениями в развитии возрастают требования к психолого-педагогической компетентности учителя. Будучи значимой и относительно самостоятельной педсистемой в структуре профессиональной компетентности, психолого-педагогическая компетентн ...

Формы и методы, которые использует педагог дополнительного образования при решении задач профессиональной ориентации
Планировать работу педагога ДО по профессиональному просвещению в школе, в частности по профпропаганде и последующей профагитации, следует в соответствии с предварительной профдиагностикой. Только на основе такого подхода можно проводить соответствующую работу со школьниками, направленную на формир ...